问题
问答题
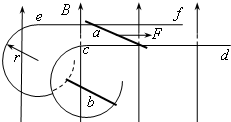
如图所示,足够长的光滑平行金属导轨cd和ef,水平放置且相距L,在其左端各固定一个半径为r的四分之三金属光滑圆环,两圆环面平行且竖直.在水平导轨和圆环上各有一根与导轨垂直的金属杆,两金属杆与水平导轨、金属圆环形成闭合回路,两金属杆质量均为m,电阻均为R,其余电阻不计.整个装置放在磁感应强度大小为B、方向竖直向上的匀强磁场中.当用水平向右的恒力F=
mg拉细杆a,达到匀速运动时,杆b恰好静止在圆环上某处,试求:3
(1)杆a做匀速运动时,回路中的感应电流;
(2)杆a做匀速运动时的速度;
(3)杆b静止的位置距圆环最低点的高度.
答案
(1)a棒匀速运动时,拉力与安培力平衡,F=BIL
得:I=
mg3 BL
(2)金属棒a切割磁感线,产生的电动势E=BLv
回路电流I=
联立得:v=E 2R 2
mgR3 B2L2
(3)b棒平衡时,设棒和圆心的连线与竖直方向的夹角为θ,
则有tanθ=
=F mg
得:θ=60°3
所以h=r(1-cosθ)=r 2
答:
(1)杆a做匀速运动时,回路中的感应电流I=
;
mg3 BL
(2)杆a做匀速运动时的速度v=
;2
mgR3 B2L2
(3)杆b静止的位置距圆环最低点的高度h=
.r 2
