如图甲所示,在虚线框两侧区域存在有大小为B、方向分别为水平向左和水平向右的匀强磁场.用薄金属条制成的闭合正方形框aa′b′b边长为L,质量为m,电阻为R.现将金属方框水平地放在磁场中,aa′边、bb′边分别位于左、右两边的磁场中,方向均与磁场方向垂直,乙图是从上向下看的俯视图.金属方框由静止开始下落,其平面在下落过程中保持水平(不计空气阻力).
(1)请根据乙图指出下落时方框中感应电流的方向;
(2)求方框下落的最大速度vm(设磁场区域在竖直方向足够长);
(3)当方框下落的加速度为
时,求方框内感应电流的功率P;g 2
(4)从静止开始经过时间t,方框下落高度为h,速度为vt(vt<vm).若在这段时间内感应电流做的功与一恒定电流I0在t时间内在该框内做的功相同,求恒定电流I0的表达式.
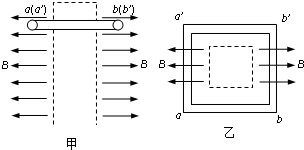
(1)金属框竖直向下运动,垂直切割磁感线,根据右手定则判断得知:感应电流的方向沿顺时针方向.
(2)最大速度时,线框做匀速运动,线框受到的安培力与重力平衡,此时线框所受的安培力大小为
F安=2 BIL=4B2L2vm R
由平衡条件得 F安=mg
联立解得 vm=mgR 4B2L2
(3)当方框下落的加速度为a=
时,g 2
根据牛顿第二定律得:ma=mg-F安=mg-2BIL
得I=mg 4BL
则方框内感应电流的功率P=I2R=m2g2R 16B2L2
(4))从静到方框下落高度为h的过程中,根据能量守恒得
mgh=
mvt2+I02Rt 1 2
解得I0=mg(H+h)-
m1 2 v 2t Rt
答:
(1)下落时方框中感应电流的方向是顺时针方向;
(2)方框下落的最大速度vm为
. mgR 4B2L2
(3)当方框下落的加速度为
时,方框内感应电流的功率P为g 2
;m2g2R 16B2L2
(4)恒定电流I0的表达式为I0=
.mg(H+h)-
m1 2 v 2t Rt

 ,
,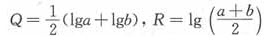 ,则()。
,则()。