如图所示,在光滑水平长直轨道上有A、B两个绝缘体,它们之间有一根长为l的轻质软线相连接,其中A的质量为m,B的质量为M=4m,A为带有电荷量为q的正电荷,B不带电,空间存在着方向水平向右的匀强电场,场强大小为E。开始时用外力把A与B靠在一起并保持静止,某时刻撤去外力,A开始向右运动,直到细线绷紧。当细线被绷紧时,两物体将有极短时间的相互作用,而后B开始运动,且细线再次松弛。已知B开始运动时的速度等于线刚绷紧前瞬间A的速度的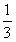 。设整个过程中,A的电荷量都保持不变。
。设整个过程中,A的电荷量都保持不变。
求细线第二次被绷紧的瞬间B对地的位移(相对于初始点)。

由动能定理得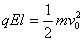
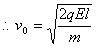 (3分)
(3分)
设细线第一次绷紧后的瞬间A的速度为v1,B的速度为v2,因细线绷紧过程所用时间极短,电场力的冲量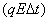 极小,可以忽略不计,根据动量守恒定律有
极小,可以忽略不计,根据动量守恒定律有
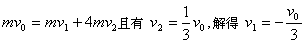 (3分)
(3分)
第一次绷紧后A的速度为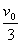 ,负号表示速度
,负号表示速度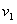 的方向水平向左,
的方向水平向左,
∴A又回到第一次绷紧的位置历时
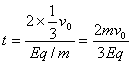
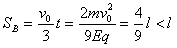
∴不会相碰 (3分)
两者速度相同时,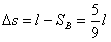 , (2分)
, (2分)
此后再运动t′绷紧: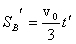
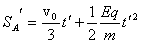 (3分)
(3分)
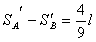 解得:
解得: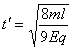
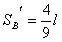 (3分)
(3分)
∴ (3分)
(3分)
