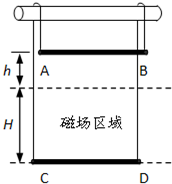
如图所示,两金属杆AB和CD长均为L,电阻均为R,质量分别为3m和m.用两根质量和电阻均可忽略的不可伸长的柔软导线将它们连成闭合回路,并悬挂在水平、光滑、不导电的圆棒两侧.在金属杆AB下方距离为h处有高度为H(H>h)匀强磁场,磁感应强度大小为B,方向与回路平面垂直,此时,CD刚好处于磁场的下边界.现从静止开始释放金属杆AB,经过一段时间下落到磁场的上边界,加速度恰好为零,此后便进入磁场.求金属杆AB
(1)进入磁场前流过的电量;
(2)释放瞬间每根导线的拉力;
(3)穿过磁场区域的过程,回路中产生的焦耳热.
(1)AB向下运动过程中,CD棒切割产生感应电动势 E=△φ △t
流过AB杆的电量 q=I△t=
△t=E 2R
=△φ 2R BLh 2R
(2)根据牛顿第二定律得
对AB棒:3mg-2T=3ma
对CD棒:2T-mg=ma
联立解得,T=
mg3 4
(3)AB棒达到磁场边界时,加速度为零,系统处于平衡状态.
对AB棒分析有 3mg=2T'.
对CD棒分析2T'=mg+BIL 即 2T′=mg+B 2L2υ1 2R
解得,此时两棒的运动速率 υ1=4mgR B2L2
此后AB棒进入磁场,系统受到安培力(阻力)突然增加,系统做加速度不断减小的减速运动,有三种可能:
一是系统减速到某一值(υ2>
)时,AB棒到磁场下边界的距离h,CD棒开始出磁场. mgR B2L2
二是系统刚好达到新的平衡点(υ2=
)时,AB棒到磁场下边界的距离h,CD棒开始出磁场. mgR B2L2
三是系统达平衡后,以υ2=
的速度匀速一段时间,AB棒到磁场下边界的距离h,CD棒开始出磁场. mgR B2L2
当AB棒以υ2≥
做变加速运动,速度增加到υ3=mgR B2L2
时,系统再次达到平衡状态,此后 AB匀速一段距离到达磁场的下边界. 4mgR B2L2
根据能量守恒可知,回路中产生的焦耳热等于系统机械能的减小,则得回路中产生的焦耳热Q=3mgH-mgH=2mgH.
答:(1)进入磁场前流过的电量是
;BLh 2R
(2)释放瞬间每根导线的拉力是
mg;3 4
(3)穿过磁场区域的过程,回路中产生的焦耳热是2mgH.