问题
问答题
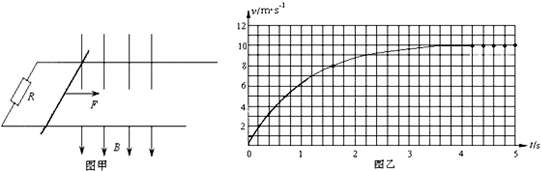
如图甲所示,放在水平桌面上的两条光滑导轨间的距离为L=1m,质量m=1kg的光滑导体棒放在导轨上,导轨左端与电阻R=4Ω的电阻相连,其它电阻不计,导轨所在位置有磁感应强度为B=2T的匀强磁场,磁场的方向垂直导轨平面向下,现在给导体棒施加一个水平向右的恒定拉力F,并每隔0、2s测量一次导体棒的速度,乙图是根据所测数据描绘出导体棒的v-t图象,(设导轨足够长)求:
(1)力F的大小;
(2)t=1.6s时,导体棒的加速度;
(3)估算1.6s电阻上产生的热量.
答案
(1)由图象可知:v=10m/s时,安培力等于拉力F
E=BLV
I=E R
F=F安=BIL=10N
(2)由图象可知,时间t=1.6s时导体棒的速度v′=8m/s,
此时导体棒上电动势E′=BLv′
导体棒受到的安培力:
F′安=BI′L=8N
由牛顿第二定律得:F-F′=ma
a=2m/s2
(3)根据动能定理得:
F•l=Q+△Ek=Q+
mv′21 2
由图象可知:位移l为t=1.6s和v-t图线及坐标轴所包围的面积,
即l=40×1×0.2m=8m
解得Q=48J.
答:(1)力F的大小是10N;
(2)t=1.6s时,导体棒的加速度是2m/s2;
(3)估算1.6s电阻上产生的热量是48J.
