如图所示，质量M="3.5" kg的小车静止于光滑水平面上靠近桌子处，其上表面与水平桌面相平，小车长L="1.2" m，其左端放有一质量为m2="0.5" kg的滑块Q。水平放置的轻弹簧左端固定，质量为m1="1" kg的小物块P置于桌面上的A点并与弹簧的右端接触。此时弹簧处于原长，现用水平向左的推力将P缓慢推至B点(弹簧仍在弹性限度内)时，推力做的功为WF，撤去推力后，P沿桌面滑动到达C点时的速度为2 m/s，并与小车上的Q相碰，最后Q停在小车的右端，P停在距小车左端S="0.5" m处。已知AB间距L1="5" cm，A点离桌子边沿C点距离L2="90" cm，P与桌面间动摩擦因数μ1=0.4，P、Q与小车表面间动摩擦因数μ2=0.1。(g="10" m/s。)求：
(1)推力做的功WF；
(2)P与Q碰撞后瞬间Q的速度大小和小车最后速度v.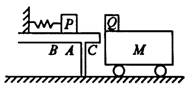
(1) WF="6J "
(2) 0.4m/s
(1)对P由A→B→C应用动能定理，得
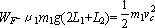
解得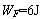
(2)设P、Q碰后速度分别为v1、v2，小车最后速度为v，由动量守恒定律得
m1vc=m1v1+-m2v2
m1vc=(m1+m2+M)v
由能量守恒得
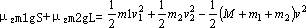
解得，v2=2m/s
v2′=
v=0.4m/s
当v2′=时，v1=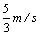
>v2′不合题意，舍去。
即P与Q碰撞后瞬间Q的速度大小为v2=2m/s
小车最后速度为0.4m/s