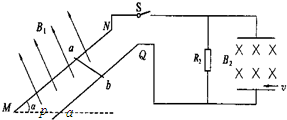
如图所示,两足够长的平行光滑的金属导轨MN、PQ相距为L=1m,导轨平面与水平面夹角α=30°,导轨电阻不计.磁感应强度为B1=2T的匀强磁场垂直导轨平面向上,长为L=1m的金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m1=2kg、电阻为R1=1Ω.两金属导轨的上端连接右侧电路,电路中通过导线接一对水平放置的平行金属板,两板间的距离和板长均为d=0.5m,定值电阻为R2=3Ω,现闭合开关S并将金属棒由静止释放,重力加速度为g=10m/s2,导轨电阻忽略不计.试求:
(1)金属棒下滑的最大速度为多大?
(2)当金属棒下滑达到稳定状态时,在水平放置的平行金属板间电场强度是多大?
(3)当金属棒下滑达到稳定状态时,在水平放置的平行金属板间加一垂直于纸面向里的匀强磁场B2=3T,在下板的右端且非常靠近下板的位置有一质量为m2,带电量为q=-1×10-4C的质点以初速度v水平向左射入两板间,要使带电质点在复合场中恰好做匀速圆周运动并能从金属板间射出,初速度v应满足什么条件?
(1)当金属棒ab匀速下滑时有m1gsinα=B1IL…①
I=
…②E R总
E=B1Lv …③
R总=R1+R2…④
联立①~④式的vm=
⑤m1gsinα(R1+R2) B12L2
得vm=10m/s
(2)由分压原理得
=B1Lvm (R1+R2)
…⑥Uc R2
将已知条件代入得UC=15V
故 E=
=30V/m 方向由上极板指向下极板 Uc d
(3)要满足题意使带电粒子做匀速圆周运动 则
=m2gUcq d
由上式可求得 m2=3×10-4㎏…⑦
根据B2qv=m2v2 r
故r=
…⑧m2v B2q
由题意分析可知,粒子的圆心在磁场的边界上,若能转回到边界处一定从右边飞出,而若半径增大,打在极板上则不会飞出;
但若半径增大到粒子从上板的左侧飞出时,也可飞出,
故要使带电粒子能从金属极板右边射出,必满足r≤
…⑨d 2
若从左边飞出,则r≥d…⑩
联立⑦⑧⑨式得v≤0.25m/s(从右边射出)
联立⑦⑧⑩式得v≥0.5m/s(从左边射出)
答:(1)最大速度为10m/s;(2)板间的场强为30V/m; (3)若从右端射出,速度≤0.25m/s,若从左端射出,速度≥0.5m/s.
