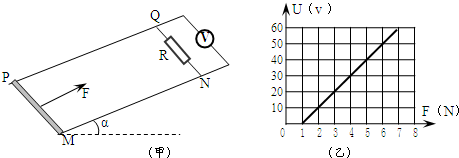
如图(甲)所示,平行的光滑金属导轨PQ和MN与水平方向的夹角α=30°,导轨间距l=0.1米,导轨上端用一电阻R相连.磁感强度为B=1T的匀强磁场垂直导轨平面向上,导轨足够长且电阻不计.一电阻r=1Ω的金属棒静止搁在导轨的底端,金属棒在平行于导轨平面的恒力F作用下沿导轨向上运动,电压表稳定后的读数U与恒力F大小的关系如图(乙)所示.
(1)电压表读数稳定前金属棒做什么运动?
(2)金属棒的质量m和电阻R的值各是多少?
(3)如金属棒以2m/s2的加速度从静止起沿导轨向上做匀加速运动,请写出F随时间变化的表达式.
(1)金属棒有外力F作用下,从静止开始做加速运动,速度增大,棒所受的安培力增大,加速度减小,最终棒受力达到平衡,所以金属棒先做加速度减小的变加速运动,最后做匀速直线运动,
(2)由图可知:当F>1时,开始产生电压,所以 mgsin30°=F=1N
则得 m=0.2Kg
当达到平衡时:感应电流I=
,F=mgsin30°+BLU R U R
得 U=
F-R BL
sin30° Rmg BL
由图象可知,
=10 R BL
解得,R=1Ω
(3)金属棒以2m/s2的加速度从静止起沿导轨向上做匀加速运动时,t时刻棒的速度V=at
感应电流 I=BLV R+r
安培力 FA=B2L2V R+r
根据牛顿第二定律得 F-FA-mgsin30°=ma
代入解得 F=1.4+0.01t(N)
答:
(1)电压表读数稳定前金属棒先做加速度减小的变加速运动,最后做匀速直线运动,
(2)金属棒的质量m和电阻R的值各是0.2kg和1Ω.
(3)如金属棒以2m/s2的加速度从静止起沿导轨向上做匀加速运动,F随时间变化的表达式为1.4+0.01t(N).
