问题
问答题
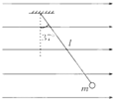
用一根长为l的丝线吊着一质量为m带电荷量为q的小球,小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成370角.现突然将该电场方向变为向下但大小不变,不考虑因电场的改变而带来的其他影响(重力加速度为g),求:
(1)匀强电场的电场强度的大小?
(2)电场方向变为向下小球经过最低点时的瞬时速度多大?
(3)电场方向变为向下小球经过最低点时丝线对小球的拉力多大?
答案
(1)以小球为研究对象,分析受力情况:重力mg、电场力qE、丝线的拉力FT,如图1所示.由平衡条件得:mgtan37°=mg
故E=3mg 4q
(2)当电场方向变为向下后,小球受到的电场力竖直向下,向下做圆周运动,重力和电场力都做正功,由动能定理得
(mg+qE)l(1-cos37°)=
mv2-01 2
解得,v=
gl7 10
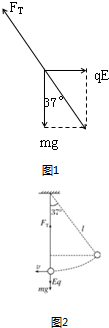
(3)小球经过最低点时,由重力、电场力和丝线的拉力的合力提供了向心力,如图2所示.根据牛顿第二定律得
FT-mg-qE=mv2 l
解得 FT=
mg49 20
答:
(1)匀强电场的电场强度的大小为
.3mg 4q
(2)电场方向变为向下小球经过最低点时的瞬时速度为
.
gl7 10
(3)电场方向变为向下小球经过最低点时丝线对小球的拉力为
mg.49 20
