如图所示,足够长的U型金属框架放置在绝缘斜面上,斜面倾角30°,框架的宽度l=1.0m、质量M=1.0kg.导体棒ab垂直放在框架上,且可以无摩擦的运动.设不同质量的导体棒ab放置时,框架与斜面间的最大静摩擦力均为Fmax=7N.导体棒ab电阻R=0.02Ω,其余电阻一切不计.边界相距d的两个范围足够大的磁场Ⅰ、Ⅱ,方向相反且均垂直于金属框架,磁感应强度均为B=0.2T.导体棒ab从静止开始释放沿框架向下运动,当导体棒运动到即将离开Ⅰ区域时,框架与斜面间摩擦力第一次达到最大值;导体棒ab继续运动,当它刚刚进入Ⅱ区域时,框架与斜面间摩擦力第二次达到最大值.(g=10m/s2).求:
(1)磁场Ⅰ、Ⅱ边界间的距离d;
(2)欲使框架一直静止不动,导体棒ab的质量应该满足的条件;
(3)质量为1.6kg的导体棒ab在运动的全过程中,金属框架受到的最小摩擦力.
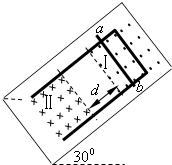
(1)导体棒即将离开Ⅰ时,金属框受到的安培力沿斜面向下,对金属框由平衡条件得
fmax=Mgsin30°+FA1max
解得,FA1max=2N
导体棒受安培力:FA1max=
,解得υ1=1m/sB2L2v1 R
导体棒刚进入Ⅱ时,金属框受到的安培力沿斜面向上,对金属框由平衡条件得
fmax′=FA2max-Mgsin30°
解得,FA2max=12N
导体棒受安培力:FA2max=B2L2v2 R
代入解得,υ2=6m/s
导体棒在两磁场边界之间运动时,mgsin30°=ma,
解得,a=5m/s2
则有d=
=3.5m
-v 22 v 21 2a
(2)导体棒离开Ⅰ之前,速度至少要达到υ1=1m/s.设此时导体棒在磁场Ⅰ中已经达到最大速度做匀速运动,
由平衡条件得:m1gsin30°=FA1max,求得m1=0.4kg
欲使金属框架不动,导体棒刚进入Ⅱ后电流不再增大,做匀速运动.由平衡条件得:
m2gsin30°=FA2max,求得m2=2.4kg
即导体棒的质量应为:0.4kg<m<2.4kg
(3)导体棒在磁场Ⅰ中运动时,由牛顿第二定律得:mgsin30°-FA1=ma
其中,FA1=B2L2υ R
导体棒做加速度减小的加速运动,最大速度为1m/s.安培力在逐渐增大,最小值是0,最大值为2N.
此过程中对金属棒,由平衡条件得f=Mgsin30°+FA1′
FA1′=FA1
可知金属框与斜面的摩擦力范围为:5N~7N.
导体棒在无场区时,金属框与斜面的摩擦力恒为5N.
导体棒在磁场Ⅱ中运动时,由牛顿第二定律得:FA2-mgsin30°=ma
又FA2=B2L2υ R
导体棒做加速度减小的减速运动,最大速度为6m/s.当a=0时,速度最小,以后做匀速运动,此时速度为4m/s.安培力在逐渐减小,最小值是8N,最大值为12N.
此过程中对金属棒,由平衡条件得:f′=FA2-Mgsin30°,FA2′=FA2
可知金属框与斜面的摩擦力范围为:3N~7N.
综上所述,金属框受到的最小摩擦力为3N.
答:
(1)磁场Ⅰ、Ⅱ边界间的距离d=3.5m;
(2)欲使框架一直静止不动,导体棒ab的质量应该满足的条件是0.4kg<m<2.4kg;
(3)质量为1.6kg的导体棒ab在运动的全过程中,金属框架受到的最小摩擦力为3N.
