如图1所示，用固定的电动机水平拉着质量m=2kg的小物块和质量M=1k

问题问答题

如图1所示，用固定的电动机水平拉着质量m=2kg的小物块和质量M=1kg的平板以相同的速度一起匀速水平向右，物块位于平板左侧，可视为质点．在平板的右侧一定距离处有台阶阻挡，平板撞上后会立刻停止．电动机功率保持P=3W．从某时刻t=0起，测得物块的速度随时间的变化关系如图2所示，求：

（1）平板与地面间的动摩擦因数μ

（2）物块在1s末和3s末两时刻受到的摩擦力各多大？

（3）若6s末物块离开平板，则平板长度L为多少？

答案

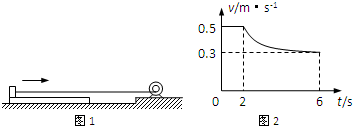
（1）在0～2s内两物体一起以0.5m/s的速度匀速运动，则有

P=F₁v₁

根据两物体匀速运动则有拉力等于摩擦力即F₁=f

而地面的摩擦力f=μN=μ（M+m）g

代入数据得μ=0.2

（2）1s时刻，物块匀速，绳子的拉力等于平板对物块的静摩擦力，

又根据平板匀速运动可知物块对平板的静摩擦力等于对面对平板的滑动摩擦力

f₁=μ（M+m）g=6N

由图可知从2s时开始平板撞到台阶上静止，故物块开始在平板上匀减速运动，故滑块所受的摩擦力为滑动摩擦力，故在静止前摩擦力的大小保持不变．

而3s时刻，物块在木板上滑动，所以滑块所受的摩擦力仍为滑动摩擦力．

因为最终物块再次匀速时速度

v₂=0.3m/s

P=F₂v₂

故F₁V₁=F₂V₂

F₂=f₂=10N

（3）物块在平板上运动的时间为t=6-2=4s，

在整个过程中电机所做的功W=Pt，摩擦力始终为滑动摩擦力大小为f₂=10N，

由动能定理

Pt-f₂L=

mv22-

v12

得L=1.216m．