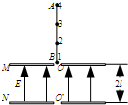
如图所示,两块相同的金属板M和N正对并水平放置,它们的正中央分别有小孔O和O′,两板间距离为2L,两板间存在竖直向上的匀强电场.AB是一长3L的轻质绝缘细杆,杆上等间距地固定着四个完全相同的带电小球(1、2、3、4),每个小球的电荷量为q、质量为m,相邻小球间的距离为L.第一个小球置于孔O处,将AB由静止释放,观察发现,从第2个小球刚进入电场到第3个小球刚要离开电场这一过程中AB杆一直做匀速直线运动,且杆保持竖直.求:
(1)两板间电场强度E;
(2)第4个小球刚要离开电场时杆的速度;
(3)从第2个小球刚进入电场开始计时,到第4个小球刚要离开电场所用的时间.
(1)从第2个小球刚进入电场到第3个小球刚要离开电场这一过程中AB杆一直做匀速直线运动,受力平衡,则有:
2qE=4mg,
E=
,2mg q
(2)从静止开始到第4个小球刚要离开电场得过程中运用动能定理得:
4mg×5L-4qE×2L=
×4mv21 2
解得:v=
,2gL
(3)设杆匀速运动时速度为v1,对第1个小球刚进入电场到第3个小球刚要进入电场这个过程,应用动能定理得:
4mg×2L-qE(L+2L)=
×4mv121 2
解得:v1=gL
第2个小球刚进入电场到第3个小球刚要离开电场这段时间,整个杆做匀速直线运动,设运动时间为t1,则:
t1=
=3L v1 3 gL g
第3个小球离开电场后,只有第4个小球在电场中,杆做匀加速直线运动,设运动时间为t2,则:
t2=
=L v1+v 2 2(
-1)2 gL g
所以总时间为:t=t1+t2=(2
+1)2 gL g
答:(1)两板间电场强度E为
;2mg q
(2)第4个小球刚要离开电场时杆的速度为
;2gl
(3)从第2个小球刚进入电场开始计时,到第4个小球刚要离开电场所用的时间为
.(2
+1)2 gL g
