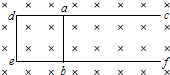
如图所示,固定在水平桌面上的光滑金属框架cdef处于竖直向下磁感应强度为B0的匀强磁场中.金属杆ab与金属框架接触良好.此时abed构成一个边长为l的正方形,金属杆的电阻为r,其余部分电阻不计.
(1)若从t=0时刻起,磁场的磁感应强度均匀增加,每秒钟增量为k,施加一水平拉力保持金属杆静止不动,求金属杆中的感应电流.
(2)在情况(1)中金属杆始终保持不动,当t=t1秒末时,求水平拉力的大小.
(3)若从t=0时刻起,磁感应强度逐渐减小,当金属杆在框架上以恒定速度v向右做匀速运动时,可使回路中不产生感应电流.写出磁感应强度B与时间t的函数关系式.
解(1)设瞬时磁感应强度为B,由题意得率
=△B △t
=k ①B-B0 △t
产生感应电动势为 E=
=△φ △t
=△BS △t
=kl2 ②(B-B0)S △t
根据闭合电路欧姆定律得,产生的感应电流I=
=E r
③kl2 r
(2)由题意,金属杆始终保持不动,根据二力平衡,安培力等于水平拉力,即有F=F安 ④
F安=BIl ⑤
由①③⑤得F按=(B0+kt1)kl3 r
所以F=(B0+kt1)kl3 r
(3)回路中感应电流为0,磁感应强度逐渐减小产生的感生电动势E和金属杆运动产生的动生电动势E′大小,方向相反,即E+E′=0,
则有
+Blv=0(B-B0)l2 t-0
解得 B=B0l l+vt
答:
(1)金属杆中的感应电流为为
.kl2 r
(2)水平拉力的大小为
.(B0+kt1)kl3 r
(3)要使回路中不产生感应电流,磁感应强度B与时间t的函数关系式为B=
.B0l l+vt
