问题
问答题
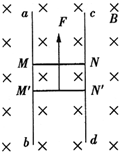
如图,ab和cd是两条竖直放置的长直光滑金属导轨,MN和M'N'是两根用细线连接的金属杆,其质量分别为m和2m.竖直向上的外力F作用在杆MN上,使两杆水平静止,并刚好与导轨接触;两杆的总电阻为R,导轨间距为l.整个装置处在磁感应强度为B的匀强磁场中,磁场方向与导轨所在平面垂直.导轨电阻可忽略,重力加速度为g.在t=0时刻将细线烧断,保持F不变,金属杆和导轨始终接触良好.求:
(1)细线少断后,任意时刻两杆运动的速度之比;
(2)两杆分别达到的最大速度.
答案
(1)细线烧断前对MN和M'N'受力分析,
由于两杆水平静止,得出竖直向上的外力F=3mg.
设某时刻MN和M'N'速度分别为v1、v2.
根据MN和M'N'动量守恒得出:mv1-2mv2=0
求出:
=2 ①v1 v2
(2)细线烧断后,MN向上做加速运动,M'N'向下做加速运动,由于速度增加,感应电动势增加,
MN和M'N'所受安培力增加,所以加速度在减小.
当MN和M'N'的加速度减为零时,速度最大.
对M'N'受力平衡:BIl=2mg ②
I=
③E R
E=Blv1+Blv2 ④
由①--④得:v1=
、v2=4mgR 3B2l2 2mgR 3B2l2
答:(1)细线少断后,任意时刻两杆运动的速度之比为2;
(2)两杆分别达到的最大速度为
,4mgR 3B2l2
.2mgR 3B2l2
