如图所示,平面直角坐标系的y轴竖直向上,x轴上的P点与Q点关于坐标原点O对称,距离为2a.有一簇质量为m、带电量为+q的带电微粒,在xoy平面内,从P点以相同的速率斜向右上方的各个方向射出(即与x轴正方向的夹角θ,0°<θ<90°),经过某一个垂直于xoy平面向外、磁感应强度大小为B的有界匀强磁场区域后,最终会聚到Q点,这些微粒的运动轨迹关于y轴对称.为使微粒的速率保持不变,需要在微粒的运动空间再施加一个匀强电场.重力加速度为g.求:
(1)匀强电场场强E的大小和方向;
(2)若一个与x轴正方向成30°角射出的微粒在磁场中运动的轨道半径也为a,求微粒从P点运动到Q点的时间t;
(3)若微粒从P点射出时的速率为v,试推导微粒在x>0的区域中飞出磁场的位置坐标x与y之间的关系式.

(1)由题意知,要保证微粒的速率不变,则微粒所受电场力与重力平衡:
qE=mg…①
解得:E=
…②方向竖直向上mg q
(2)设A、C分别为微粒在磁场中运动的射入点和射出点,根据题意画出微粒的运动轨迹如图所示根据几何关系可得:
=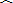
AC
2πa…③2θ 360°
PA=
atanθ…④a cosθ
设微粒运动的速率为v,由牛顿定律:
qvB=m
…⑤v2 a
微粒从P点运动到Q运动的路程为s,则:
s=2PA+
AC…⑥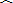
AC
t=s v
联解③④⑤⑥得:
t=
…⑦(2
+π)m3 3qB
(3)根据题意作出粒子在x>0区域内的运动示意如图所示,设微粒飞出磁场位置为C,在磁场中运动的轨道半径为r,根据牛顿定律和几何关系可得:
qBv=m
…⑧v2 r
x=rsinθ…(⑨
y=(
-rtanθ)sinθ …⑩a cosθ
联解(⑧⑨⑩)得:
y=
…(14)Bq(ax-x2) m2v2-B2q2x2
答案为:(1匀强电场场强:E=
,方向竖直向上mg q
(2)微粒从P点运动到Q点的时间:t=(2
+π)m3 3qB
(3微粒在x>0的区域中飞出磁场的位置坐标x与y之间的关系式:y=Bq(ax-x2) m2v2-B2q2x2
