问题
选择题
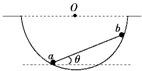
两个可视为质点的小球a和b,用质量可忽略的刚性细杆相连,放置在一个光滑的半球面内,如图所示.己知小球a和b的质量之比为
,细杆长度是球面半径的3
倍.两球处于平衡状态时,细杆与水平面的夹角θ是( )2
A.45°
B.30°
C.22.5°
D.15°
答案
设细杆对两球的弹力大小为T,小球a、b的受力情况如图所示,
其中球面对两球的弹力方向指向圆心,即有cos α=
=
R2 2 R 2 2
解得:α=45°
故FNa的方向为向上偏右,即β1=
-45°-θ=45°-θπ 2
FNb的方向为向上偏左,即β2=
-(45°-θ)=45°+θπ 2
两球都受到重力、细杆的弹力和球面的弹力的作用,过O作竖直线交ab于c点,设球面的半径为R,由相似三角形可得:
=mag OC FNa R
=mbg OC FNb R
解得:FNa=
FNb; 3
取a、b及细杆组成的整体为研究对象,由平衡条件得:水平方向上有:
FNa•sin β1=FNb•sin β2
即 FNa•sin(45°-θ)=FNb•sin(45°+θ)
解得:θ=15°.
故选D.

