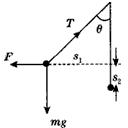
如图甲所示,质量为m=50g,长l=10cm的铜棒,用长度亦为l的两根轻软导线水平悬吊在竖直向上的匀强磁场中,磁感应强度B=0.5T.未通电时,轻线在竖直方向,通入恒定电流后,棒向外偏转的最大角度θ=37°,求此棒中恒定电流的大小.同学甲的解法如下:对铜棒进行受力分析,通电时导线向外偏转,说明安培力方向垂直电流和磁场方向向外,受力如图乙所示(侧视图).
当最大偏转角θ=37°时,棒受力平衡,有:tanθ=
=F mg BIl mg
得I=
=mgtan370 Bl
=7.5A0.05×10× 3 4 0.5×0.1
同学乙的解法如下:铜棒向外偏转过程中,导线拉力不做
功,如图丙所示.
F做功为:WF=FS1=BIlsin370×lsin370
重力做功为:WG=-mgS2=-mgl(1-cos37°)
由动能定理得:BI(lsin37°)2-mgl(1-cos37°)=0I=
=mgl(1-cos370) Blsin2370
=0.05×10×(1-0.8) 0.5×0.1×(0.6)2
=5.56A50 9
请你对同学甲和乙的解答以说理的方式作出评价;若你两者都不支持,则给出你认为正确的解答.

(1)甲和乙同学的解法均错误
错误原因:前者认为棒到达最高点速度为零时,一定处于平衡状态,或者认为偏角最大的是平衡位置;后者将安培力做功求错.
(2)正确的解法如下:金属棒向外偏转过程中,导线拉力不做功,如图所示:安培力F做功为WF=FS1=BIL2sin37°
重力做功为WG=-mgS2=-mgL(1-cos37°)
由动能定理得BIL2sin37°-mgL(1-cos37°)=0
解得 I=
=5Amg(1-cos37°) BLsin37°
答:此棒中恒定电流的大小为5A.
