在竖直平面内固定一半径为R的金属细圆环,质量为m的金属小球(视为质点)通过长为L的绝缘细线悬挂在圆环的最高点.当圆环、小球都带有相同的电荷量Q(未知)时,发现小球在垂直圆环平面的对称轴上处于平衡状态,如图所示.已知静电力常量为k.则下列说法中正确的是( )
A.电荷量Q=mgL3 kR
B.电荷量Q=mg(L2-R2) 3 2 kR
C.绳对小球的拉力F=mgR L
D.绳对小球的拉力F=mgL L2-R2 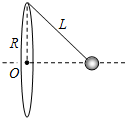
由于圆环不能看作点电荷,我们取圆环上一部分△x,设总电量为Q,则该部分电量为
Q;△x 2πR
由库仑定律可得,该部分对小球的库仑力F1=
,方向沿该点与小球的连线指向小球;KQ△XQ 2πL2R
同理取以圆心对称的相同的一段,其库仑力与F1相同;如图所示,
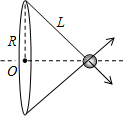
两力的合力应沿圆心与小球的连线向外,大小为2
×KQ△XQ 2πL2R
=L2-R2 L
; KQ2△ X L2-R2 πL3R
因圆环上各点对小球均有库仑力,故所有部分库仑力的合力F库=
×πR=KQ2 L2-R2 πL3R
,方向水平向右;KQ2 L2-R2 L3
小球受力分析如图所示,小球受重力、拉力及库仑力而处于平衡,故T与F的合力应与重力大小相等,方向相反;
由几何关系可得:
=T L
; mg R
则小球对绳子的拉力T=
,故C、D错误;mgL R
=F L2-R2
; mg R
则F=
=mg L2-R2 R
; KQ2 L2-R2 L3
解得Q=
; mgL3 kR
故A正确,B错误;
故选A.





