问题
问答题
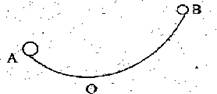
如图，竖直平面内有一半径足够大光滑圆弧形轨道，O为最低点，A、B两点距O点的高度分别为h和4h，现在从A点释放一质量为M的大物体，且每隔适当的时间从B点释放一质量为m的小物体，它们和大物体碰撞后都结为一体，已知M=100m。
（1）若每当大物体向右运动到O点时，都有一个小物体与之碰撞，问碰撞多少次后大物体速度最小？
（2）若每当大物体运动到O点时，都有一个小物体与之碰撞，若碰撞50次后大物体运动的最大高度为h的几分之几？
答案
(1) n=50次(2)
（1）设分别由A、B释放的物理沿圆弧轨道运动到O点时速度大小分别为VA、VB。
由机械能守恒定律得：
20081208 |
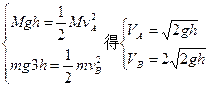设n次碰撞后大物体速度最小，出动量守恒定律得：MvA-nmvB=（M+nm）vmin
当MvA-nmvB=0时，大物体速度最小
解得n=50次
（2）第1次碰撞：MvA-nmvB=（M+m）v1
第2次碰撞：（M+m）v1+ mvB=（M+2m）v2
第3次碰撞：（M+2m）v2+ mvB=（M+3m）v3
第4次碰撞：（M+3m）v3+ mvB=（M+4m）v4
| |
| |
第50次碰撞：（M+49m）v49+ mvB=（M+50m）v50
两边相加得：MvA=（M+50m）v50
解得：v50=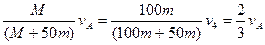
由机械能守恒定律得：
（M+50m）gh′=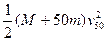
解得：