问题
问答题
设f(x1，x2，…，xn)=xTAx是一实二次型，若有实n维向量x1，x2，使f(x1)=
，证明：存在n维向量x0≠0，使
．
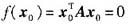答案
参考答案：本题考查二次型．题目提法新颖，有一定的综合性和分析意味，具有一定的难度．
由于有实n维向量x1，x2，使
[*]
所以f(x1，x2，…，xn)=xTAx是不定二次型，故存在可逆线性变换x=Py，使
[*]
其中1≤p＜r≤n，取
[*]
令x0=Py0，则x0≠0，且有
[*]