问题
问答题
如图所示，质量为M=4kg的木板放置在光滑的水平面上，其左端放置着一质量为m=2kg的滑块(视作质点)，某时刻起同时给二者施以反向的力，如图，已知F1=6N，F2=3N，
适时撤去两力，使得最终滑块刚好可到达木板右端，且二者同时停止运动，已知力F2在t2=2s时撤去，板长为S=4.5m，g=10m/s2，求
(1) 力F1的作用时间t1
(2) 二者之间的动磨擦因数μ
(3) t2=2s时滑块m的速度大小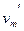
答案
（１）t1=1s（２）μ=0.1（３）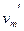
=1m/s
(1) 以向右为正， 对整体的整个过程，由动量定理得
F1t1-F2t2="0 " 代入数据得t1=1s
(2) 在t1时间内，对m，由F合=ma得 F1-μmg=mam 代入数据可得am=2m/s2
m在t1时间内的位移大小S1=
am t12 代入数据得 S1=1m
同理在t2时间内，对M有 F2-μmg=MaM 代入数据得 aM=0.25m/s2
M在t2时间内的位移大小S2=aM t22 代入数据得 S2=1m
整个过程中，系统的机械能未增加，由功能关系得 F1S1+F2S2-μmgs="0 "
代入数据得μ=0.1
(3) 在t2=2s内，m先加速后减速，撤去F1后，m的加速度大小为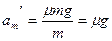
=1m/s2
所以m在t2=2s时的速度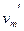=amt1-
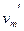(t2-t1) 代入数据得=1m/s