[说明]
对于数学上一个猜想：任何自然数平方的36倍等于两对孪生素数的和。初始的情形如下：
1²×36=(5+7)+(11+13)
2²×36=(29+31)+(41+43)
3²×36=(11+13)+(149+151)
再往下，N取4，5，6，时，只要N不太大，也都可以找到N(上标)2×36等于两对孪生素数的和。但是当N是一个任意的正整数时，证明N²×36总是等于两对孪生素数的和，这还是一个目前尚未解决的问题。甚至当考察的数较大时，找出一组符合条件的两对孪生素数都是计算量相当大的工作。每尝试一次，都要作4次是否是素数的判断，要作许多次的尝试，才可能找到一组解。下面流程图设计了一种优化算法来对这个猜想进行验证。仔细阅读流程图8-11，完成程序部分。

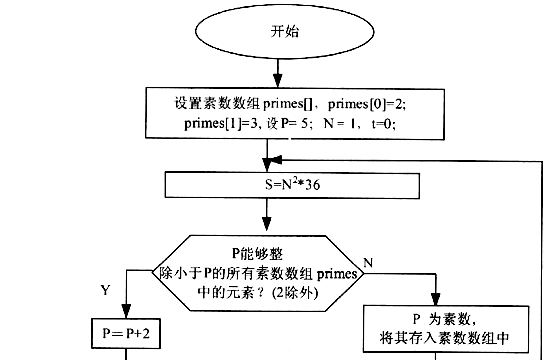
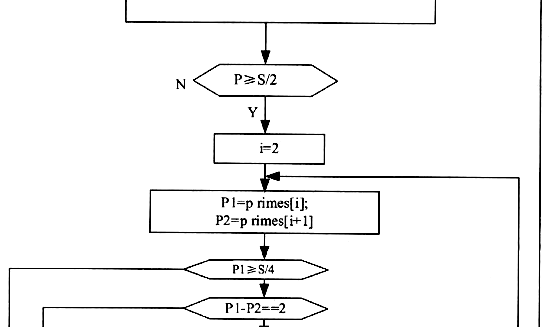
图8-11
[程序部分]
main ()

int t, i, j, prime_index; is_p rime:
long n, p, p1, p2, p3, p4, s, s1;
long primes [ 16000 ];
for (n=1; n＜98; ++n) t=0;
s= n* n* 36;
prime_index= 2;
primes[0]=2; primes[1]=3;
for (p=5: p＜=s/2; p=p+2)

is_p rime= 1;
for ( i=1; (1) ++i)
if ( p%primes [i] = = 0 ) is_p rime= 0;
if ( is_p rime)

(2)


for ( i=1; (3) ++i)

(4)
if ( p2=p1+ 2 )

s1=s- (p1+p2)
p3=sl/2-1; p4=p3+2:
for ( j=0; j＜=prime_index-1; ++j )
if ( (5) )

printf ( "%d* % d*36= (%d+ %d) + (%d+%d) \n", \ n,n, p1, p2, p3, p4 ) ;
++t;



if ( t! = 0 ) printf ("%d\n", t )
else
printf ( "%d* %d*36=no so lution\n ", n, n ) ;