试题四（共15 分）阅读下列说明，回答问题1 至问题2，将解答填入答题纸的对应栏内。【说明】0-1 背包问题可以描述为：有n 个物品，对i=1,2,···,n，第i 个物品价值为vi,重量为wi(vi 和wi 为非负数），背包容量为W(W 为非负数)，选择其中一些物品装入背包，使装入背包物品的总价值最大，即

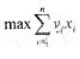,且总重量不超过背包容量，即

,其中，xi∈{0,1}, xi=0 表示第i 个物品放入背包。

【问题2】（7 分）考虑表4-1 的实例，假设有3 个物品，背包容量为22。图4-1 中是根据上述算法构造的搜索树，其中结点的编号表示了搜索树生成的顺序，边上的数字1/0 分别表示选择/不选择对应物品，除了根结点之外，每个左孩子结点旁边的上下两个数字分别表示当前背包的重量和已获得的价值，右孩子结点旁边的数字表示扩展了该结点后最多可能获得的价值。为获得最优解，应该选择特(5),获得的价值为(6). 表4-1 0-1 背包问题实例

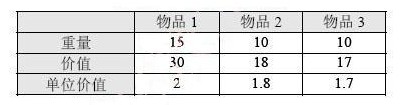
于表4-1 的实例，若采用穷举法搜索整个解空间，则搜索树的结点数为（7），而用了上述的回溯法，搜索树的结点的为（8）。