问题
问答题
设f(x)在(-∞,+∞)上连续,证明f(x)是以l(>0)为周期的周期函数的充要条件是
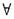 a∈(-∞,+∞)恒有
a∈(-∞,+∞)恒有
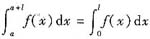 ;
;
答案
参考答案:本题是一元积分学的综合题,是一道有一定难度的综合题.
证明必要性
设[*]
由题设φ’(a)=f(a+l)-f(a)=0[*]φ(a)=c(常数).
设[*].
充分性
对[*],两边对a求导,得f(a+l)-f(a)=0[*]f(x)以l为周期.
设f(x)在(-∞,+∞)上连续,证明f(x)是以l(>0)为周期的周期函数的充要条件是
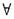 a∈(-∞,+∞)恒有
a∈(-∞,+∞)恒有
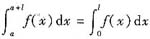 ;
;
参考答案:本题是一元积分学的综合题,是一道有一定难度的综合题.
证明必要性
设[*]
由题设φ’(a)=f(a+l)-f(a)=0[*]φ(a)=c(常数).
设[*].
充分性
对[*],两边对a求导,得f(a+l)-f(a)=0[*]f(x)以l为周期.