问题
问答题
如图所示。质量为m的小球A放在光滑水平轨道上，小球距左端竖直墙壁为s。另一个质量为M=3m的小球B以速度v0沿轨道向左运动并与A发生正碰，已知碰后A球的速度大小为1.2v0，小球A与墙壁的碰撞过程中无机械能损失，两小球均可视为质点，且碰撞时间极短。求：（1）两球发生第一次碰撞后小球B的速度大小和方向。（2）两球发生碰撞的过程中A球对B球做功的大小。（3）两球发生第二次碰撞的位置到墙壁的距离
答案
（1）0.6 v0 ；方向与B球碰撞前的速度方向相同 （2）0.96mv02 （3）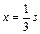
（1）A、B两球碰撞过程动量守恒，即Mv0=MV+mv （2分）
根据已知：M=3m，v = 1.2v0解得V = 0.6 v0
方向与B球碰撞前的速度方向相同。（3分）
（2）A球对B球所做功的大小等于B球动能的减少量
所以A球对B球所做功的大小为：W=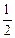
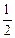Mv02-MV2=0.96mv02………（3分）
（3）设A、B两球发生第二次碰撞的位置距墙壁为x，则A球以1.2v0的速度运动的距离为s+x，B球以0.6 v0运动的距离为s – x，A、B两球运动的时间相等，…（3分）
则有：
…………（3分）
解得两球发生第二次碰撞的位置距墙壁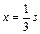： …………（2
分）