问题
问答题
设函数f(x)在(-∞，+∞)有界且导数连续，又对于任意实数x有｜f(x)+f’(x)｜≤1．
试证明：｜f(x)｜≤1．
答案
参考答案：[证] 作辅助函数F(x)=exf(x)，则F’(x)=ex[f(x)+f’(x)]．
得｜F’(x)｜≤ex，即-ex≤F’(x)≤ex，则有
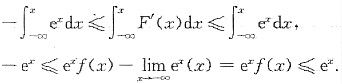
故-1≤f(x)≤1，即｜f(x)｜≤1．
搜题请搜索小程序“爱下问搜题”
设函数f(x)在(-∞，+∞)有界且导数连续，又对于任意实数x有｜f(x)+f’(x)｜≤1．
试证明：｜f(x)｜≤1．
参考答案：[证] 作辅助函数F(x)=exf(x)，则F’(x)=ex[f(x)+f’(x)]．
得｜F’(x)｜≤ex，即-ex≤F’(x)≤ex，则有
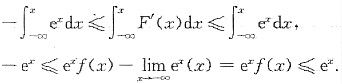
故-1≤f(x)≤1，即｜f(x)｜≤1．