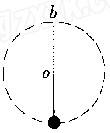
如图所示的装置中，两个光滑定滑轮的半径很小，表面粗糙的斜面固定在地面上。现用一根伸长量可以忽略的轻质细绳跨过定滑轮连接可视为质点的甲、乙两物体，其中甲放在斜面上且连线与斜面平行，乙悬在空中，放手后，甲、乙均处于静止状态。当一水平向右飞来的子弹击中乙（未穿出）后，子弹立即和乙一起在竖直平面内来回运动，若乙在摆动过程中，悬线偏离竖直方向的最大偏角为α＝60°，整个过程中，甲均未动，且乙经过最高点（此时乙沿绳方向的合外力为零）和最低点时，甲在斜面上均即将滑动。已知乙的重心到悬点O的距离为l＝0.9 m，乙的质量为m乙＝0.99kg，子弹的质量m＝0.01 kg，重力加速度g取10m/s2，求：
（1）子弹射入射己前的速度大小；
（2）斜面对甲的最大静摩擦力。
（1）300m/s（2）7.5N
（1）设子弹射入物块前的速度大小为v0，射入后共同速度的大小为v，
子弹击中乙的过程中动量守恒，有 mv0＝（m＋m乙）v ① （3分）
乙上摆到最高点的过程，机械能守恒
有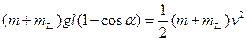
② （3分）
联立②③解得 v0＝300m/s （2分）
（2）设甲物体的质量为m甲，说受的最大静摩擦力为f，斜面的倾角为θ，
当乙物体运动到最高点时，绳子上的弹力设为T1，
T1＝（m＋m乙）gcosθ ③ （2分）
此时甲物体恰好不下滑，有 m甲g sinθ＝f＋T1 ④ （2分）
当乙物体运动到最低点时，绳子上的弹力设为T2，
由牛顿第二定律：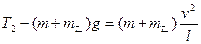
⑤ （2分）
此时甲物体恰好不上滑，有 m甲g sinθ＋f＝T2 ⑥ （2分）
联立②③④⑤⑥解得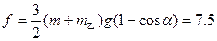 
N （3分）