问题
问答题
设f(x)在[a,b]上连续,在(a,b)内可导.试证明:
若再添设f(x)不是一次式的条件,则至少存在一点ξ∈(a,b)使|f’(ξ)|>
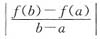 .
.
答案
参考答案:作φ(x)如上,并且不妨设f(b)-f(a)≥0.因f(x)不是一次式,故至少存在一点x1∈(a,b)使
[*]
或至少存在一点x2∈(a,b)使
[*]
设为前者,在区间[a,x1]上对φ(x)用拉格朗日中值定理,存在ξ1∈(a,x1)[*](a,b),使
[*]
即 [*]
从而知存在ξ1∈(a,b)使
[*]
设为后者,在区间[x2,b]上对φ(x)用拉格朗日中值定理,存在ξ2∈(x2,b)[*](a,b),使
[*]
即[*]
不论哪种情形皆有[*],若f(b)-f(a)<0,证明类似.
