问题
问答题
设方程组
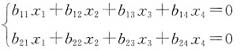 (*)
(*)
有通解k1ξ1+k2ξ2=k1[1,2,1,-1]T+k2[0,-1,-3,2]T.
方程组
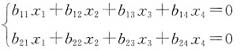 (**)
(**)
有通解 λ1η1+λ2η2=λ1[2,-1,-6,1]T+λ2[-1,2,4,a+8]T.
已知方程组
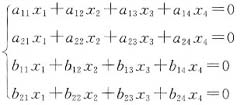 (***)
(***)
有非零解,试确定参数a的值,并求该非零解.
答案
参考答案:(Ⅲ)有非零解,即(Ⅰ)、(Ⅱ)有非零公共解,设为β,则β是属于(Ⅰ)的通解,也是属于(Ⅱ)的通解,即
β=k1ξ1+k2ξ2=λ1η1+λ2η2,其中k1,k2,λ1,λ2均不全为零.
得 k1ξ1+k2ξ2-λ1η1-λ2η2=0, (*)
(*)有非零解[*]r(ξ1,ξ2,-η1-η2)<4.
对[ξ1,ξ2,-η1,-η2]作初等行变换.
[*]
[*]
r(ξ1,ξ2,-η1,-η2)<4[*]a=-8.
故当a=-8时,方程组(Ⅲ)有非零解.
当a=-8时,方程组(*)的系数矩阵经初等行变换为
[*]
方程组(*)有解
[k1,k2,λ1,λ2]=k[1,1,l,1].
故方程组(Ⅰ),(Ⅱ)的公共解为
[*]
[*]
其中k是任意常数.
