设f(x)在(-∞，+∞)上连续，下述命题 ①若对任意a，，则f(x)必

问题单项选择题

设f(x)在(-∞，+∞)上连续，下述命题
①若对任意a，

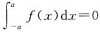，则f(x)必是奇函数．
②若对任意a，

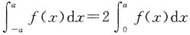，则f(x)必是偶函数．
③若f(x)为周期T的奇函数，则

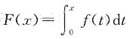也具有周期T．正确的个数是( )．

答案

参考答案：D

解析：

[分析]： ①是正确的：记[*]，有F’(a)=f(a)+f(-a)．由于F(a)=0，所以F’(a)≡0，所以f(a)=-f(-a)，f(x)为奇函数．
②是正确的：记[*]，F’(a)=f(a)+f(-a)-2f(a)≡0，所以f(-a)=f(a)，推知f(x)为偶函数．
③[*]
所以F(x)具有周期T．选(D)．