问题
问答题
已知函数f(x)在(-1，1)上有定义，
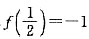，当且仅当0＜x＜1时，f(x)＜0，且对任意x、y∈(-1，1)，都有
．
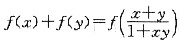求证：f(x)在(-1，1)上单调递减．
答案
参考答案：
先证f(x)在(0，1)上单调递减.
令0 )
∵0
∴
>0,又(x2－x1)－(1－x2x1)=(x2－1)(x1+1)<0
∴x2－x1<1－x2x1,∴0<
<1,
由题意知f(
)<0，即f(x2)
∴f(x)在(0，1)上为减函数，又f(x)为奇函数且f(0)=0.
∴f(x)在(－1，1)上为减函数.