某市政工程网络双代号计划图已经总监理工程师批准执行,如下图所示。
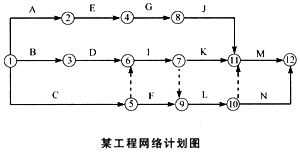
各下作相关数据如下表所示。
各工作相关数据表
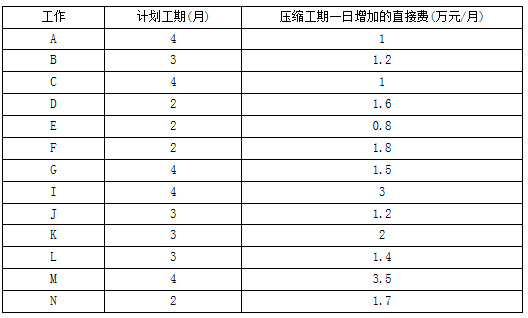
问题
1.计算此工程的计划工期,说明A、C、D、I、J的ES、EF、TF,并确定关键线路。
2.若A、I、J三工序共用一台设备,用图示说明A、I、J依次顺序施工计划情况,并计算设备在场时间,确定该工序关键线路与总工期。
3.施工过程中由于设计变更,C工作增加3个月;由于乙方施工出现重大质量事故,D工作完成后决定返修增加用工2个月;在K、J工作完成后M工作开始前增加工作O,工期1个月,费用变动率为 3万元;说明关键线路是否发生变化共用设备在场时间是否发生变化
4.施工指挥部决定在问题3中事件发生的前提下要求按原计划工期完土,施工组织以最小变动费用为目标应如何调整并计算相应增加的费用。调整工序作业时间限定每个关键工序只能减少1天。
参考答案:
1.计算如下图所示。
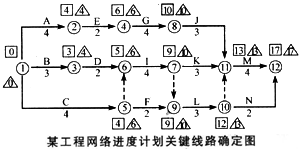
经计算A—E—G—J—M工作组成关键线路,计划工期为17个月。
A工序ES=0,EF=4,TF=0;C工序ES=0,EF=4,TF=2; D工序ES=3,EF=5,TF=1;I工序ES=5,EF=9,TF=1; J工序ES=10,EF=13,TF=0。
2.计算如下图所示。 关键线路和计划工期不变,由于A工序ES=0,J工序EF=14,所以设备在场时间为13个月。
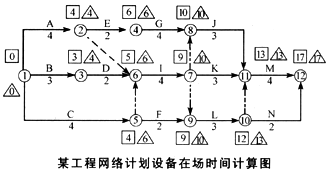
3.计算如下图所示。
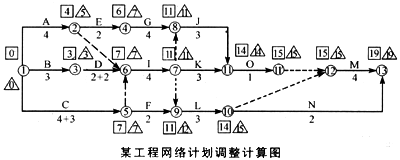
由上图可知,关键线路发生变化, * * 生四条关键线路,
即: B—D—I—K—O—M; B—D—I—J—O—M C—I—K—O—M;C—I—J—O—M
A工序ES=0,J工序EF=13所以设备在场时间为14个月,增加1个月。
4.C工作、D工作工作时间延误致使总工期变为19个月,若保证按原计划17个月完工,就需对7月份以后施工工序中的关键工序进行压缩,由于O工作为新增加工作工期仅1个月,无法压缩。
由于J工序与K工序为平行的关键工序,仅压缩其中一个工序的工期,总工期不能改变。 在压缩关键工序工作时间时应每次减少1个单位时间,如果关键线路不发生改变仍按原线路压缩。若关键线路发生改变,应考虑在新的关键线路上进行压缩,压缩过程如下表所示。

结论:按照最小变动费用为目标确保17个月完工的调整方案为I、J、K三工序均压缩工期1个月。调整后增加的费用为6.2万元。
