问题
问答题
在极坐标曲线r=eθ的
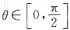范围内的曲线上找一点，使经过它的切线．与x轴，y轴的正向所围成的三角形的面积为最小，并求出此最小面积的值．
答案
参考答案：将极坐标曲线r=eθ化成参数式x=rcosθ=eθcosθ，y=rsinθ=eθsinθ，在任意一点处的切线斜率为[*]，在θ处的切线方程为
[*]
在两坐标轴上的截距
[*]
三角形面积
[*]
当[*]时Y＜0或无定义，故θ应满足[*]．
[*]
命[*]，得tan2θ=-1，[*]，当[*]时，[*]；当[*]时，[*]，所以当[*]时A为极小，且此时为唯一驻点，故当[*]时A为最小．
[*]
