问题
单项选择题
下列命题
①设
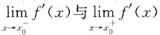均存在，则f(x)在x=x0处必连续．
②设f’-(x0)与f’+(x0)均存在，则f(x)在x=x0处必连续．
③设
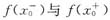均存在，则f(x)在x=x0处必连续．
④设
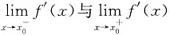中至少有一个不存在，则f(x)在x=x0必不可导．正确的个数是( )．
答案
参考答案：A
解析：
[分析]： f’-(x0)存在，即f(x)在x=x0处左导数存在，推知f(x)在x=x0处左连续；f’+(x0)存在，推知f(x)在x=x0处右连续．故f(x)在x=x0处连续．②正确．
①与③都不正确，因为这两种情形，f(x0)可以没有定义．
④也不正确，反例如下：
[*]
可知
[*]
[*]不存在，但f’(x0)却存在．