问题
单项选择题
设函数f(u,v)具有一阶连续偏导数,且f(x+y,x-y)=4(x2-xy-y2),则xf’x(x,y)+yf’y(x,y)=
(A) 2x2-8xy一2y2. (B) -2x2+8xy-2y2.
(C) 2x2-8xy+2y2. (D) -2x2+8xy+2y2.
答案
参考答案:D
解析: 首先求出函数f(x,y)的表达式.令u=x+Y,v=x-y则可解得
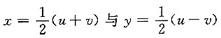 ,代入即得
,代入即得
f(x+y,x-y)=f(u,v)=(u+v)2-(u+v)(u-v)-(u-v)2
=-u2+4uv+v2.
于是f(x,y)=-x2+4xy+y2.求偏导数即得
f’x(x,y)=-2x+4y,f’y(x,y)=4x+2y,
故
xf’x(x,y)+yf’y(x,y)=x(-2x+4y)+y(4x+2y)=-2zx2+8xy+2y2.
即应选(D).
