问题
问答题
某饮料厂生产的一种果汁，1994～2003年的广告费支出与销售量的统计资料如表2-1所示。 2004年计划将广告费提高到150万元，试建立回归模型并预测销售量以便于制定2004年年度的生产计划。
表2-1
| 年份 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 |
| 广告费支出x(万元) | 10 | 20 | 40 | 50 | 60 | 80 | 70 | 110 | 110 | 140 |
| 销售量y(万箱) | 20 | 30 | 35 | 40 | 50 | 70 | 65 | 80 | 75 | 95 |
(1)计算相关系数(直线回归方程)。
(2)计算TSS、RSS、ESS、R2。
(3)进行相关系数检验(a=0.01)，t检验(a=0.01)、F检验(a=0.05)。
(4)预测2004午销售量及预测区间(a=0.05)。
答案
参考答案：
：
经计算可得到下表(n=10)。
表2-5
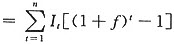所以回归直线方程
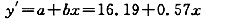
相关系数
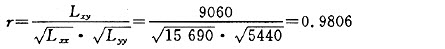
问题(2)：
由表2-5可知：
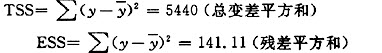
RSS=TSS-ESS=5440-141.11=5298.89(回归平方和)
R2=RSS/TSS=5298.89/5440=0.97(可决系数)
问题(3)：
①相关系数检验：
n=10，n-2=8，r0.01=0.765，r=0.9806＞r0.01=0.765
说明所建立的回归模型线性关系高度显著；
②t检验：
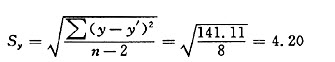
参数b标准差
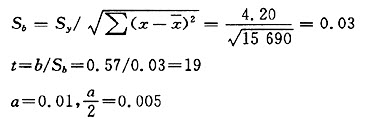
所以t检验通过，变量x和y之间线性假设合理。
③F检验：
F=R2(n-2)/(1-R2)=0.97×8/0.03=258.67
f0.05(1，8)=5.32
因为F＞Fa(1，n-2)
所以在d=0.05的显著性检验水平上，F检验通过。说明预测整体水平可靠性高。
问题(4)：
已知x0＝150，所以
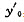=16.19+0.57×150=101.69(万箱)。预计2004年产量为101.69万箱(点预测)。
在a=0.05显著水平上，2004年产量预测区间为(
)，即(101.69±2.306×5.17)，即产量在89.76～113.61万箱之间(区间预测)。
[解题思路]
一元线性回归预测方法是咨询工程师考试中的重要题型，即是重点内容也是难点内容，学员应注意此题中的关键内容：回归方程建立；预置值(区间)的计算；检验方法的应用。此题的难点是TSS、 RSS、ESS的计算。解题时要注意对基本数据的分析和基本条件应用的前提。