问题
问答题
已知矩阵
 可逆,A*是A的伴随矩阵,
可逆,A*是A的伴随矩阵,
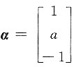 是A*的特征向量.
是A*的特征向量.
(Ⅰ)求A*的特征值与特征向量;
(Ⅱ)判断A*能否相似对角化,如能则求可逆矩阵P使P-1A*P=A,如不能则说明理由.
答案
参考答案:按定义,设A*α=λ0α,则AA*α=λ0Aα,即λ0Aα=|A|α由于矩阵A可逆,知|A|≠0,λ0≠0,于是
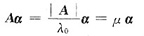
对于
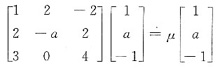
即
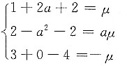 解出μ=1,a=-1.
解出μ=1,a=-1.
由矩阵A的特征多项式
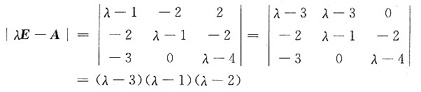
得矩阵A的特征值是1,2,3.于是|A|=6.从而A*的特征值是6,3,2.
对λ=1,由(E-A)x=0
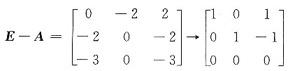
得矩阵A属于特征值λ=1的特征向量是α1=(-1,1,1)T.于是A*属于特征值λ=6的特征向量是k1α1,(k1≠0).
对λ=2,由(2E-A)x=0

得矩阵A属于特征值λ=2的特征向量α2=(-2,2,3)T,于是A*属于特征值λ=3的特征向量是k2α2,(k2≠0).
对λ=3,由(3E-A)x=0
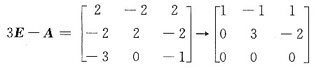
得矩阵A属于特征值λ=3的特征向量α3=(-1,2,3)T,于是A*属于特征值λ=2的特征向量是k3α3,(k3≠0).
(Ⅱ)因为A*有3个线性无关的特征向量,故A*~A.
令
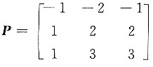 则有
则有
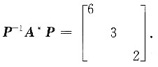
[评注] 若已知特征向量α,通常可用定义法建立方程组来求参数.本题不必去求伴随矩阵A*,而应当用关系式AA*=A*A=|A|E把A*的特征值问题转化为A的特征值问题。
