问题
问答题
某市计划投资150(百万元)对该地区现有电器厂和化工厂进行技术改造．已知为完成一个电器厂的技术改造需要投资5(百万元)，而完成一个化工厂的技术改造需要投资6(百万元)．一旦x个电器厂与y个化工厂完成技术改造，并在扣除这些厂的技术改造的投资后可使该市得到总利润的年增加值为
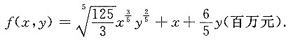问该地区应当使用这笔资金分别改造多少个电器厂和化工厂，才能使该地区得到总利润年增加值最大，且最大值是多少
答案
参考答案：
[分析]： 本题主要考查条件极值的求法，是经济中的最大值应用问题．
目标函数是总利润年增加值函数f(x，y)，要在5z+6y=150的约束条件下求f(x，y)的最大值，其中x和Y分别是完成技术改造的电器厂和化工厂的个数．
[解法一] 利用拉格朗日乘数法求解．令
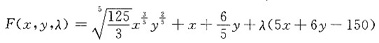
驻点条件是
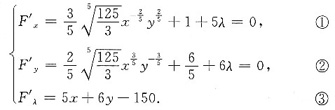
由①，②可得
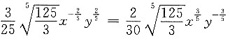，即9y=5x．
结合③可解出唯一驻点x=18，y=10．
因驻点唯一，且实际问题必存在最大值，故上述结果表明该地区应改造18个电器厂和10个化工厂，可获得最大总利润年增加值，且此最大值为
maxf=f(18，10)=60(百万元)．
[解法二] 从约束条件5x+6y=150可得
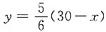，代入目标函数有
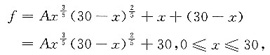
其中
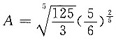.由驻点条件
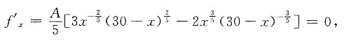
可解得唯一驻点x=18．又因
于是f当x=18时(且y=10时)取得极大值，注意f在定义域内部仅有唯一驻点且取极大值，因此在x=18技术改造可获得最大利润年增加值，其最大值为f(18，10)=60(百万元)．
