问题
单项选择题
设α1=(1，0，2，c1)T，α2=(0，2，1，c2)T，α3=(1，2，3，c3)T，α4=(1，0，1，0)T其中ci(i=1，2，3)为任意实数，则
(A) α1，α2，α3，α4必线性相关． (B) α1，α2，α3，α4必线性无关．
(C) α1，α2，α3必线性相关． (D) α1，α2，α3，必线性无关．
答案
参考答案：D
解析： 如(B)正确则(D)必正确，因此(B)不正确．若(C)正确则(A)必正确，故(C)必错误，所以正确的在(A)或(D)中．
由于
仅当c1+c2=c3时，α1，α2，α3，α4才线性相关，故(A)不正确．
所以选(D)．
或者，由
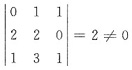，知(0，2，1)T，(1，2，3)T，(1，0，1)T必线性无关，从而α2，α3，α4必线性无关．而知(D)必正确．