问题
解答题
| 在△ABC中,角A,B,C的对边分别是a,b,c,且b2=ac=a2-c2+bc. (1)求
(2)试判断△ABC的形状,并说明理由. |
答案
(1)∵b2=a2-c2+bc,即b2+c2-a2=bc,
∴由余弦定理得:cosA=
=b2+c2-a2 2bc
,1 2
又A为三角形的内角,
∴A=
,…(3分)π 3
又b2=ac,即c=
,b2 a
∴
=bsinB c
=absinB b2
,asinB b
由正弦定理
=a sinA
得:sinA=b sinB
,asinB b
∴
=sinA,又sinA=asinB c
,3 2
则
=bsinB c
; …(7分)3 2
(2)△ABC为等边三角形,理由如下:…(9分)
证明:不失一般性,可设c=1,
∵b2=ac=a2-c2+bc,
∴b2=a=a2+b-1,
消去a得:b2=b4+b-1,即(b-1)(b3+b2+1)=0,
∵b3+b2+1≠0,
∴b-1=0,即b=1,
∴a=b2=1,
∴a=b=c=1,
则△ABC为等边三角形.…(14分)

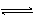 4NO(g) + 6H2O(g),下列叙述正确的是( )
4NO(g) + 6H2O(g),下列叙述正确的是( )