Rewrite the following sentences as required(根据所给要求,改写下列句子。每空格限填一词)
小题1:Peter has bread and milk for breakfast.(改为否定句)
Peter_______ _________bread or milk for breakfast.
小题2:Mr. Smith and his wife seldom drive their car to work.(改为反意疑问句)
Mr. Smith and his wife seldom drive their car to work,______ ______?
小题3:You should take the medicine three times a day.(对划线部分提问)
________ ________should you take the medicine?
小题4:London will hold the next Olympic Games.(保持句意基本不变)
The next Olympic Games will _______ ______in London.
小题5:My grandpa began to learn how to use a computer when he was over sixty.(保持句意不变)
My grandpa began to learn how to use a computer in ______ ______.
小题6:Chinese people plant a large number of trees on March l2 every year.(改为被动语态)
A 1arge number of trees _______ ______on March 12 every year.
小题7:"Are you doing your homework, Tom?" Mother asked.(把直接引语改为间接引语)
Mother asked Tom ______he _____doing his homework.
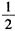 )。
)。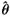 ,讨论其无偏性,一致性。
,讨论其无偏性,一致性。