问题
问答题
设总体X是离散型随机变量,可能取值为0,1,2,而X1,X2,…,X3是来自总体X的简单随机样本,如果P(X=2)=(1-θ)2,E(X)=2(1-θ)(其中θ是未知参数,且0<θ<
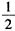 )。
)。
求X的分布律;
答案
参考答案:记P0=P(X=0),p1=P(X=1),p2=p(X=2),已知p2=(1-θ)2,E(X)=2(1-θ),则
[*]
从而p0=θ2,p1=2θ(1-θ)
故X的分布律为
| X
|
