问题
问答题
设某企业的生产函数为Q(K,L)=5KL,其中投入要素L的价格为10单位,投入要素K的价格为2单位,若产品售价为10单位且有市场需求时,试分别求出当投入要素受约束和不受约束情况下的最优投入量L*、K*(当投入要素受约束时可只给出求解的式子)。
答案
参考答案:解:企业的利润函数为π(L,K)=eQ-C(L,K)=50KL-(10L+2K)
(1)投入要素受约束情况下的最优投入量
投入要素受约束时,假设约束为企业的可支配收入W,则有:
maxPQ(L,K)-C(L,W)
s.t.10L+2K≤W
拉格朗日函数为:
π(L,K)=50KL-(10L+2K)+λ(W-10L-2K)
拉格朗日定理认为,最优选择必定满足以下三个一阶条件:
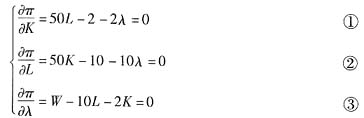
由①②③式可得:
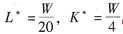 。
。
(2)投入要素不受约束情况下的最优投入量
π(L,K)=PQ-C(L,K)=50KL-(10L+2K)
其一阶条件为:
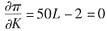 ④
④
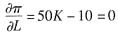 ⑤
⑤
由④⑤式可得:L*=0.04,K*=0.2。
