1994年某地区木材消费量为20万吨,主要应用于建筑业、家具制造业等行业,1995~2002年当地木材消费量及同期第二产业产值如表6-2所示,2003~2007年第二产业增长速度预计为10%。相关系数见表6-3~表6-5。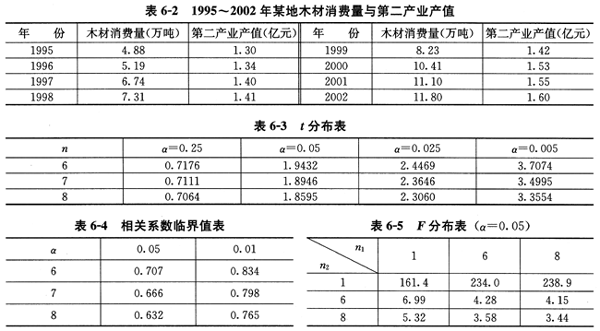
【问题】1. 用一元回归方法预测2007年当地木材需求量。
参考答案:
建立回归模型
经过分析,发现该地区木材消费量与第二产业产值之间存在线性关系,将木材消费量设为因变量y,以第二产业产值为自变量x,建立一元回归模型:y=a+bx
(2)参数计算
采用最小二乘法;计算出相关参数

(3)相关检验
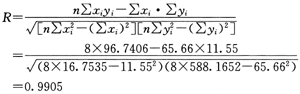
在a=0.05自由度n-2=6,查相关检验表得R0.05=0.707
R=0.9905>R0.05=0.707
故在a=0.05的显著性检验水平上,检验通过。相关系数计算见表6-11。
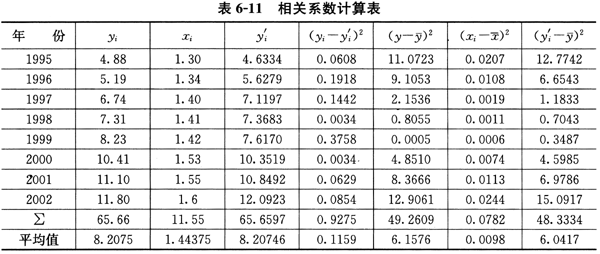
(4)t检验
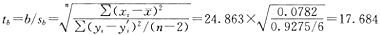
在a=0.05时自由度=n-2=6,查t检验表得t(0.025,6)=2.4469
∵tb=17.684>t(0.025,6)=2.4469
∴在a=0.05的显著性检验水平上,t检验通过。
(5)F检验
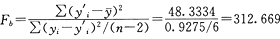
在a=0.05,自由度n1=1,n2=n-2=6,查F检验表得F(1,6)=6.99
∵Fb>F(1,6)=6.99 ∴F检验通过
(6)需求预测
2007年第二产业产值将达到:x(2007)=(1+r)5x(2002)
=(1+10%)5×1.60
=2.577(亿元)
2007年当地木材需求量预测:
y(2007)=a+bx(2007)=-27.6885+24.863×2.577=36.383(万吨)
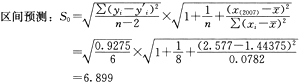
在a=0.05的显著性检验水平上,2007年木材需求量的置信区间为:
36.383±t(0.025,6) S0=36.383±16.88
即在(19.503,53.263)的区间内。
解析:
一元线性回归方法预测

