试题四(共 15 分)阅读下列说明和图,回答问题1 至问题3,将解答填入答题纸的对应栏内。【说明】某机器上需要处理 n 个作业job1, job2, …, jobn,其中:(1) 每个作业jobi(1≤i≤n)的编号为i,jobi 有一个收益值p[i]和最后期限值d[i];(2) 机器在一个时刻只能处理一个作业,而且每个作业需要一个单位时间进行处理,一旦作业开始就不可中断,每个作业的最后期限值为单位时间的正整数倍;(3) job1~jobn 的收益值呈非递增顺序排列,即p[1]≥p[2]≥…≥p[n];(4) 如果作业jobi 在其期限之内完成,则获得收益p[i];如果在其期限之后完成,则没有收益。为获得较高的收益,采用贪心策略求解在期限之内完成的作业序列。图4-1 是基于贪心策略求解该问题的流程图。(1) 整型数组J[]有n 个存储单元,变量k 表示在期限之内完成的作业数,J[1..k]存储所有能够在期限内完成的作业编号,数组J[1..k]里的作业按其最后期限非递减排序,即d[J[1]]≤ … ≤d[J[k]]。(2) 为了方便于在数组J 中加入作业,增加一个虚拟作业job0,并令d[0] = 0,J[0]= 0。(3) 算法大致思想:先将作业job1 的编号1 放入J[1],然后,依次对每个作业jobi(2≤i≤n)进行判定,看其能否插入到数组J 中,若能,则将其编号插入到数组J 的适当位置,并保证J 中作业按其最后期限非递减排列,否则不插入。jobi 能插入数组J 的充要条件是:jobi 和数组J 中已有作业均能在其期限之内完成。(4) 流程图中的主要变量说明如下:i:循环控制变量,表示作业的编号;k:表示在期限内完成的作业数;r:若jobi 能插入数组J,则其在数组J 中的位置为r+1;q:循环控制变量,用于移动数组J 中的元素。
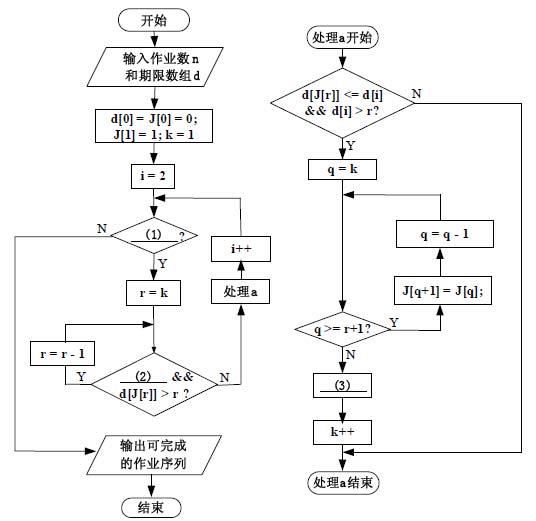 图4-1 贪心策略流程图
图4-1 贪心策略流程图
【问题 3】(2 分)对于本题的作业处理问题,用图4-1 的贪心算法策略,能否求得最高收益? (6) 。用贪心算法求解任意给定问题时,是否一定能得到最优解? (7) 。
参考答案:(6) 能 (7) 不能
