问题
单项选择题
下列命题
① 若
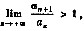 则
则
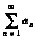 发散
发散
② 若
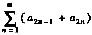 收敛,则
收敛,则
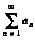 收敛
收敛
③ 若
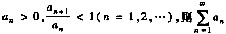 收敛
收敛
④ 设an>0(n=1,2,…),并存在极限
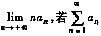 收敛,则
收敛,则

中正确的是
答案
参考答案:D
解析:[分析一] 这4个命题中有两个正确,两个错误,因此只须断定其中的两个是正确的或错误的即可.
易知命题②是错误的,即添加了括号后的级数
[*]
收敛,推不出原级数收敛.例如
[*]
发散,但[*]
命题③也是错误的.对于正项级数[*]不能保证[*]可能有[*]此时比值判别法失效.如[*]发散.
因此①,④正确.故应选(D).
[分析二] 显然①是正确的.由于[*]自然数N,当n>N时[*]这表明n>N时an同号,不妨设an>0,这正是正项级数比值判别法的极限形式,由
[*]
[*]发散.
对于命题④,同样由比较原理的极限形式,因[*]极限
[*]
若l≠0,则[*]发散.因而由[*]收敛,得l=0,即[*],故命题④正确.
综上分析,应选(D).
