问题
问答题
假定一个竞争性厂商，其生产函数为：Q=F(K，L)=AKαLβ，生产要素L和K的价格分别为W和r。
(1)试求在K为不变投入时厂商的短期成本函数；
(2)求厂商的长期成本函数，并讨论不同的规模报酬对平均成本曲线形状的影响。
答案
参考答案：解：(1)在短期，假设K保持在K0水平不变，则生产函数为：Q=F(K0，L)=AKα0Lβ，因而可得劳动投入与产出之间的关系为：
。
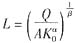因此，短期成本函数为：
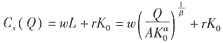
(2)在长期内，劳动和资本都可以改变，因而厂商的成本最小化问题为：
CL(Q)=minwL+rk
S．t．AKαLβ≥Q
设拉格朗日函数为：
L=wL+rK+λ(Q-AKαLβ)
成本最小化的一阶条件为：
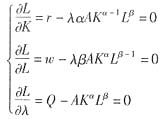
从而可以解得：
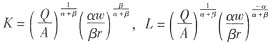
从而可得长期成本函数为：
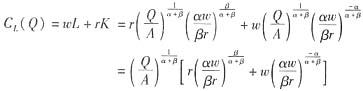
平均成本为：
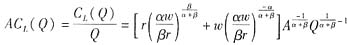
对于柯布一道格拉斯生产函数而言，α+β＞1时，规模报酬递增；当α+β=1时，规模报酬不变；当α+β＜1时，规模报酬递减。
因此，当α+β＞1，即规模报酬递增时，
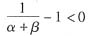，从而随着产量的递增，平均成本减少，平均成本曲线因而向下倾斜；当α+β＜1，即规模报酬递减时，
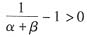，从而随着产量的递增，平均成本递增，平均成本曲线因而向上倾斜；当α+β=1，即规模报酬不变时，
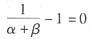，从而平均成本不受产量的影响，平均成本曲线因而是一条水平的直线。
