问题
问答题
设生产函数为
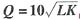，式中a为产量，L和K分别为不同的生产要素，设L和K的投入价格为PL=50元，PK=80元，试求：
(1)试写出边际产量函数；
(2)如果生产400个单位的产品，应投入L和K各多少才能使成本最低此时成本是多少
(3)如果总投入为600元，应投入L和K各多少才能使产量最大此时最大产量是多少
答案
参考答案：解：(1)生产函数为：
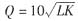
劳动的边际产量函数为：
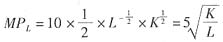
资本的边际产量函数为：
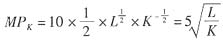
(2)根据厂商利润最大化的要素使用原则
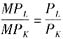，即有：
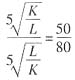
解得：
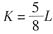
当Q=400时，代入生产函数，可得：
。
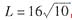则
。
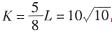最小成本为：
。
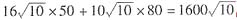(3)如果总投入为600元，则可得成本函数为：600=50L+80K，另已求得厂商利润最大化时劳动投入数量和资本投入数量的比例，即
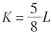。故可得：L=6，K=3.75。
最大产量
。