参考答案：证明：已知劳动的产出弹性

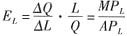，资本的产出弹性

。
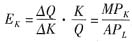(1)由F(L，K)=AK^αL^β可得：
MP_L=βAK^αL^β-1，AP_L=AK^αL^β-1
MP_K=αAK^α-1L^β，AP_K=AK^α-1L_β
所以，

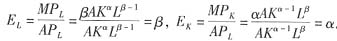可知：当生产函数具有Cobb-Dauglas的形式时，劳动和资本的产出弹性为常数。
(2)设E_L=β，E_K=α，其α、β均为常数。则有

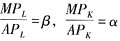，即：
MP_L·L=β·AP_L·L=β·F(L，K)
MP_K·K=α·AP_K·K=α·F(L，K)
其中F(L，K)=AP_L·L=AP_K·K为生产函数。所以，

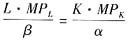，即αL．

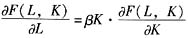，解此二元微分方程可得：
F(L，K)=AK^αL^β(A为常数)
综合(1)、(2)，可得劳动和资本的产出弹性为常数当且仅当生产函数具有Cobb-Dau-glas的形式时即F(L，K)=AK^αL^β。