问题
问答题
设f(x)在[0，2]内二阶连续可导，且f(1)=0，证明：
(Ⅰ)
(Ⅱ)
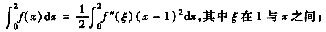
(Ⅲ)
答案
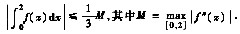
参考答案：[分析与证明] (Ⅰ)这里用二阶导数来表示定积分值，一个自然的想法是用分部积分法．按要证的结论(也为了利用条件f(1)=0)，先将[0，2]上的积分表成[0，1]上的积分与[1，2]上的积分之和．
[*]
[*]
(Ⅱ)函数与其二阶导数之间的关系可用一阶泰勒公式来描述．因此，另一自然的想法是用泰勒公式．由于题中给出条件f(1)=0，我们考虑f(x)在x=1处的带拉格朗日余项的一阶泰勒公式，即
[*]
其中ξ在1与x之间．于是
[*]
(Ⅲ)用题(Ⅰ)的结论，有
[*]
或用题(Ⅱ)的结论，有
[*]
[*]